Большинство алгоритмов многомерного шкалирования рассчитаны на использование симметричной матрицы близостей (сходств или различий), в которой выполняется условие равенства расстояний между точками, независимо от направления перехода d(a,b)=d(b,a). Однако существует множество ситуаций, когда это условие нарушается. Сюда относятся социометрия, исследования товарооборота между странами, взаимного цитирования, социальной мобильности, переключения между брендами и т. п. Очевидно, что различия в цитировании друг друга парой научных журналов могут нести важную информацию об относительном статусе этих журналов. Таким образом, специальное изучение асимметрии дистанционных матриц представляет интерес, по крайней мере, в случае неравноправных социальных отношений. В связи с этим, был предложен ряд моделей асимметричного многомерного шкалирования, обзор которых представлен, например, в работе [Cox & Cox, 2001]. В данной работе будет предложена очень простая интерпретация асимметричных матриц, позволяющая применять к ним классические алгоритмы неметрического многомерного шкалирования. На модельных данных будет показана валидность этой интерпретации.
Предположим, что асимметрия расстояний возникает из‑за неоднородности пространства, в котором они измеряются. Это легко себе представить на примере машины, едущей в гору (рис. 1).
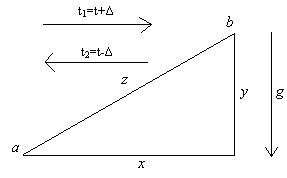
Рисунок 1. Пример неоднородного пространства
Для того чтобы преодолеть расстояние x, ей необходимо затратить время t(x), причем t(x(a,b))=t(x(b,a)). Но, в случае движения автомобиля по наклонной плоскости, при одинаковой силе тяги, t(z(a,b))>t(z(b,a)). Поскольку в измерении y действует гравитационное поле. Если бы мы захотели использовать время прохождения пути z в качестве меры расстояния между a и b, то получили бы асимметричную матрицу из двух элементов t1 и t2. Первый из них превосходил бы второй, поскольку t1=t+Δ, а t2=t-Δ, где t — это время прохождения без учета силы тяжести, а Δ — поправка на эту силу. Очевидно, что t=(t1 + t2)/2, а Δ=(t1 – t2)/2. Это соответствует разложению матрицы расстояний на симметричный и несимметричный компоненты (оба из которых являются симметричными матрицами), предложенному в работе [Constantine & Gower, 1978]. Очевидно также, что Δ монотонно связана с расстоянием y, а t — с расстоянием x. Из этого следует, что симметричный компонент может быть подвергнут неметрическому многомерному шкалированию, и аналогичную процедуру можно осуществить с асимметричным компонентом. Получившиеся во втором случае измерения могут быть интерпретированы как пространство, в котором действуют силовые поля.
Предлагаемый нами подход можно резюмировать следующим образом:
1.Необходимо разложить асимметричную матрицу на симметричный и несимметричный компоненты.
2.Подвергнуть симметричный компонент многомерному шкалированию с помощью одного из неметрических алгоритмов.
3.Подвергнуть несимметричный компонент многомерному шкалированию с помощью одного из неметрических алгоритмов.
4.Совместить результаты шкалирования симметричного и несимметричного компонентов в одном пространстве.
5.Интерпретировать измерения симметричного компонента как свободные от силовых полей, несимметричного компонента — как динамические измерения.
Для того, чтобы проверить валидность предложенной интерпретации, расширим наш простой пример с двумя точками. На рисунке 2 представлен путь, который необходимо преодолеть автомобилю при движении из пункта 1 в пункт 10 и обратно. Начальная скорость автомобиля в каждой точке равна нулю.

Рисунок 2. Неоднородное пространство с множеством точек
Углы склонов, обозначенные на рисунке, составляют соответственно, 43°, –40°, 48°, –39°, 42°, –46°, 45°, –49°, 38°. Высоты точек равны 500, 1000, 300, 1500, 200, 3000, 600, 2100, 400 и 4500 метров. Масса автомобиля m=1500 кг, сила тяги F=15*103H, g=9,82 м/с2. Согласно второму закону Ньютона, ускорение при подъеме вычисляется по формуле
![]()
ускорение при спуске по формуле
![]()
Время, затрачиваемое на прохождение одного склона, определяется следующим образом:

где s — длина склона.
Произведя вычисление времени прохождения автомобиля между всеми точками в одну и другую сторону, мы получили асимметричную матрицу временных затрат:
Таблица 1.
Асимметричная матрица временных затрат
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0 | 21,1 | 32,6 | 67,2 | 83,2 | 132,6 | 152,4 | 189,6 | 205,7 | 263,7 |
| 2 | 9,4 | 0 | 11,6 | 46,1 | 62,1 | 111,5 | 131,3 | 168,5 | 184,6 | 242,7 |
| 3 | 33,7 | 24,3 | 0 | 34,6 | 50,6 | 100 | 119,7 | 157 | 173,1 | 231,1 |
| 4 | 47,3 | 38 | 13,7 | 0 | 16 | 65,4 | 85,2 | 122,4 | 138,5 | 196,5 |
| 5 | 80,2 | 70,9 | 46,6 | 32,9 | 0 | 49,4 | 69,2 | 106,4 | 122,5 | 180,6 |
| 6 | 102,7 | 93,3 | 69 | 55,4 | 22,5 | 0 | 19,8 | 57 | 73,1 | 131,2 |
| 7 | 150,4 | 141 | 116,7 | 103 | 70,1 | 47,7 | 0 | 37,3 | 53,3 | 111,4 |
| 8 | 166,2 | 156,8 | 132,5 | 118,9 | 86 | 63,5 | 15,8 | 0 | 16 | 74,1 |
| 9 | 207,9 | 198,5 | 174,2 | 160,6 | 127,7 | 105,2 | 57,5 | 41,7 | Средняя оценка 0 / 5. Количество оценок: 0
Сожалеем, что вы поставили низкую оценку! Позвольте нам стать лучше! Расскажите, как нам стать лучше? Похожие работы
Современное общество — это общество высоких технологий. Интернет охватил весь мир и все сферы жизнедеятельности людей. Интернет-магазины дают возможность совершать Рефлексия как процесс самопознания всегда вызывала интерес у многих мыслителей еще со времен античной философии. Аристотель определял рефлексию как «мышление, На протяжении всей истории заселения северных территорий миграция играла исключительно важную роль. Нет такой области, республики или населенного пункта, где Дискриминация в трудовых отношениях остается одной из самых «острых» социальных проблем внутригосударственного и мирового масштаба. Дискриминация (discrimination) в переводе с |